Abstract
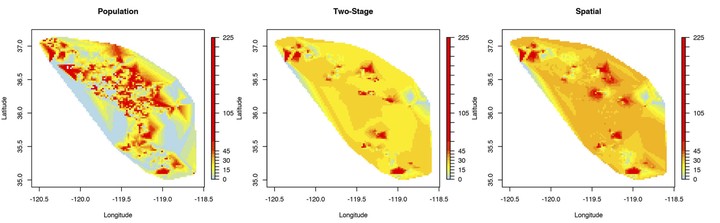
We develop a Bayesian model–based approach to finite population estimation accounting for spatial dependence. Our innovation here is a framework that achieves inference for finite population quantities in spatial process settings. A key distinction from the small area estimation setting is that we analyze finite populations referenced by their geographic coordinates. Specifically, we consider a two-stage sampling design in which the primary units are geographic regions, the secondary units are point-referenced locations, and the measured values are assumed to be a partial realization of a spatial process. Estimation of finite population quantities from geostatistical models does not account for sampling designs, which can impair inferential performance, whereas design-based estimates ignore the spatial dependence in the finite population. We demonstrate by using simulation experiments that process-based finite population sampling models improve model fit and inference over models that fail to account for spatial correlation. Furthermore, the process-based models offer richer inference with spatially interpolated maps over the entire region. We reinforce these improvements and demonstrate scalable inference for groundwater nitrate levels in the population of California Central Valley wells by offering estimates of mean nitrate levels and their spatially interpolated maps.