Abstract
There has been a growing interest in the application of social network theory to the epidemiology of sexually-transmitted diseases (STD). This interest arises from recognition that STDs are transmitted through binary contacts and, consequently, predictions about STD epidemics are unlikely to be robust to the mass-action assumptions of classical mathematical epidemiology.
Substantial attention has recently been given to the possibility that human sexual networks exhibit scale-free behavior. We consider scale-free networks that arise when the probability mass function for partner number (i.e., network degree) is given by a power law, $P(k) \approx k^{−\alpha}$ , with $2 < \alpha \le 3$. Such networks are characterized by a degree distribution with infinite variance, and since the epidemic threshold parameter increases linearly with the variance under behavioral heterogeneity, the epidemic threshold should always be exceeded in such a scale-free system.
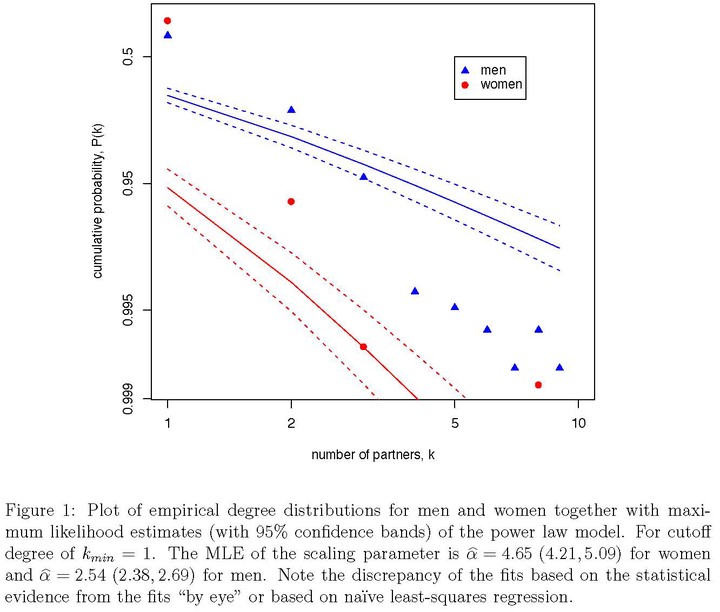
We derive the maximum likelihood estimator for the scaling exponent in the discrete power-law distribution, and show that the statistical fit of the power-law model is very poor for a large local network data set from Uganda. This finding suggests that human sexual networks may be more complex than simple analogy to computer networks might suggest, and that a more flexible, actor-based approach to modeling sexual networks is required to understand and control STD epidemics.