Abstract
Recent research into the properties of human sexual contact networks has suggested that the degree distribution of the contact graph exhibits power-law scaling. One notable property of this power-law scaling is that for a range of scaling exponents, the variance of the degree distribution is infinite.
This property is of fundamental significance for the control of sexually transmitted diseases (STDs) such as HIV/AIDS since infinite variance of the degree distribution implies no epidemic threshold, and that an STD can persist regardless of its transmissibility. A stochastic process, known as preferential attachment, that yields one form of power law scaling has been suggested to underlie the scaling of sexual degree distributions.
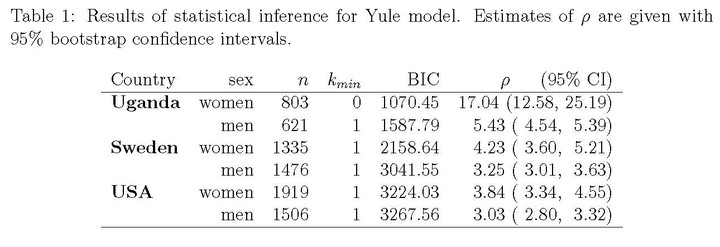
The limiting distribution of the preferential attachment process is the Yule distribution, which we fit using maximum likelihood (ML) to local network data for samples of three populations: (1) the Rakai District, Uganda, (2) Sweden, and (3) USA.
For all local networks but one, our interval estimates of the scaling parameters do not overlap the range in which Yule distribution has infinite variance. The exponent for male networks in the USA is close to the infinite-variance range, but the preferential attachment model is a very poor fit to these data.
We conclude that epidemic thresholds exist in both single-sex and two-sex epidemic model formulations. A strong conclusion we derive from these results is that public health interventions aimed at reducing the transmissibility of STD pathogens, such as implementing condom use or high activity anti-retroviral therapy (HAART), have the potential of bringing a population below the epidemic transition, even in populations exhibiting large degrees of behavioral heterogeneity.