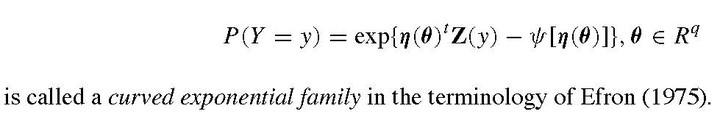
Abstract
Network data arise in a wide variety of applications. Although descriptive statistics for networks abound in the literature, the science of fitting statistical models to complex network data is still in its infancy. The models considered in this article are based on exponential families; therefore, we refer to them as exponential random graph models (ERGMs). Although ERGMs are easy to postulate, maximum likelihood estimation of parameters in these models is very difficult. In this article, we first review the method of maximum likelihood estimation using Markov chain Monte Carlo in the context of fitting linear ERGMs. We then extend this methodology to the situation where the model comes from a curved exponential family. The curved exponential family methodology is applied to new specifications of ERGMs, proposed by Snijders et al. (2004), having non-linear parameters to represent structural properties of networks such as transitivity and heterogeneity of degrees. We review the difficult topic of implementing likelihood ratio tests for these models, then apply all these model-fitting and testing techniques to the estimation of linear and non-linear parameters for a collaboration network between partners in a New England law firm.