Abstract
This is a paper in the ‘Dynamic Social Network Modeling and Analysis’, edited by R. Breiger, K. Carley, and P. Pattison. It is the result of the Committee on Human Factors, Board on Behavioral, Cognitive, and Sensory Sciences. National Academy Press: Washington, DC. DOI: 10.17226/10735.
This paper presents recent advances in the statistical modeling of random graphs that have an impact on the representation of social networks. We also consider issues related to the estimation of random graph models. For concreteness the focus is cross-sectional social networks.
Statistical exponential family models (Wasserman and Pattison, 1996) are a generalization of the Markov random graph models introduced by Frank and Strauss (1986), which in turn derived from developments in spatial statistics (Besag, 1974). These models recognize the complex dependencies within relational data structures.
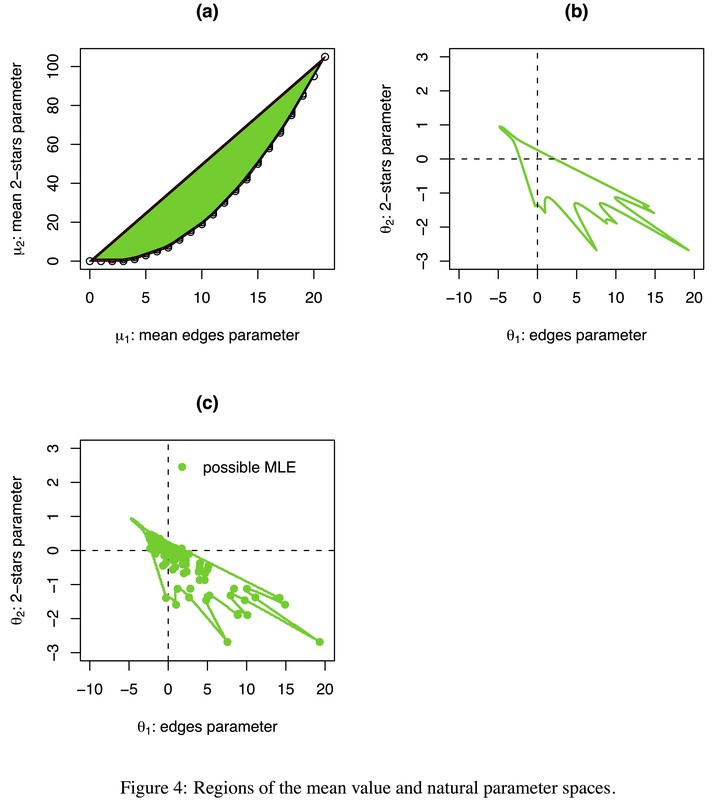
To date, the use of stochastic graph models for networks has been limited by three interrelated factors: the complexity of realistic models, lack of use of simulation studies, and a poor understanding of the properties of inferential methods.
We discuss these factors and related issues of the degeneracy of inference for commonly promoted models. As a cornerstone of this development we present a Markov Chain Monte Carlo (MCMC) algorithm for general random graph models. We also review the role of these MCMC algorithms in simulation, likelihood-based inference, identifying degeneracy of inference, and Bayesian formulations.