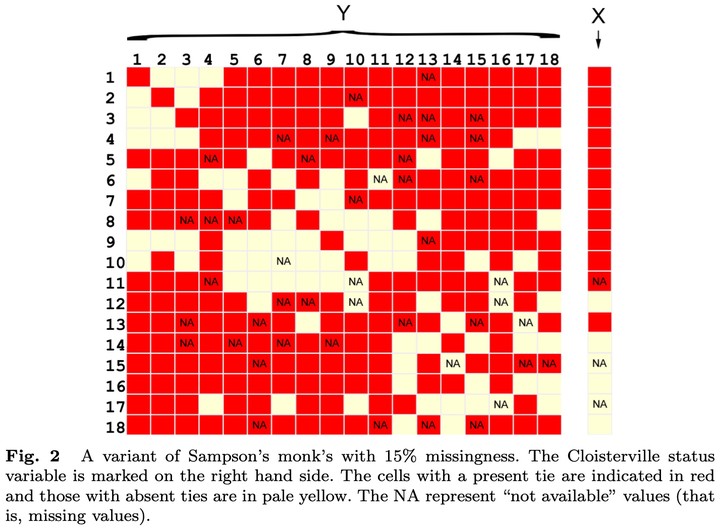
Abstract
Networked populations consist of inhomogeneous individuals connected via relational ties. The individuals typically vary in multivariate attributes. In some cases primary interest focuses on individual attributes and in others the understanding of the social structure of the ties. In many circumstances both are of interest, as is their relationship. In this paper we consider this last, most general, case. We model the joint distribution of social ties and individual attributes when the population is only partially observed. Of central interest is when the population is surveyed using a network sampling design. A second situation is when data about a subset of the ties and/or the individual attributes is unintentionally missing.
Exponential-family random network models (ERNM)s are capable of specifying a joint statistical representation of both the ties of a network and individual attributes. This class of models allow the nodal attributes to be modeled as stochastic processes, expanding the range and realism of exponential-family approaches to network modeling. In this paper we develop a theory of inference for ERNMs when only part of the network is observed, as well as specific methodology for partially observed networks, including non-ignorable mechanisms for network-based sampling designs. In particular, we consider data collected via contact tracing, of considerable importance to infectious disease epidemiology and public health.