Abstract
This is a paper as part of the reviewed proceedings of the ICML 2006 Workshop on Statistical Network Analysis, entitled ‘Statistical Network Analysis: Models, Issues, and New Directions’ published in the Lecture Notes in Computer Science Series.
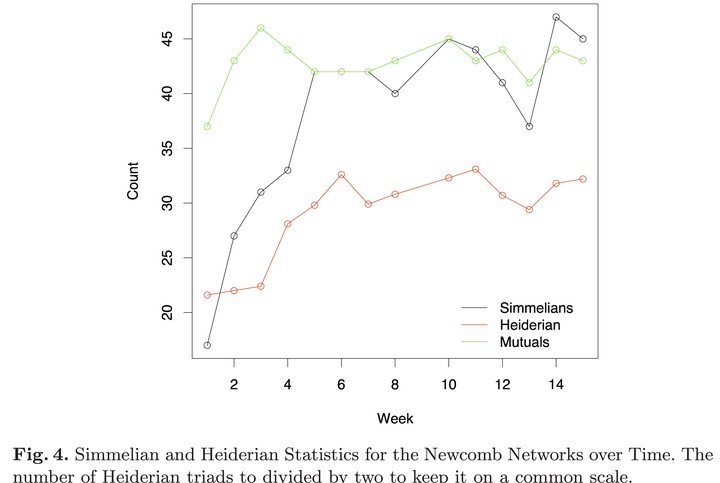
Heider’s balance theory is ubiquitous in the field of social networks as an explanation for why we so frequently observe symmetry and transitivity in social relations. We propose that Simmelian tie theory could explain the same phenomena without resorting to motivational tautologies that characterize psychological explanations. Further, while both theories predict the same equilibrium state, we argue that they suggest different processes by which this equilibrium is reached. We develop a dynamic exponential random graph model (ERGM) and apply it to the classic panel data collected by Newcomb to empirically explore these two theories. We find strong evidence that Simmelian triads exist and are stable beyond what would be expected through Heiderian tendencies in the data.