Abstract
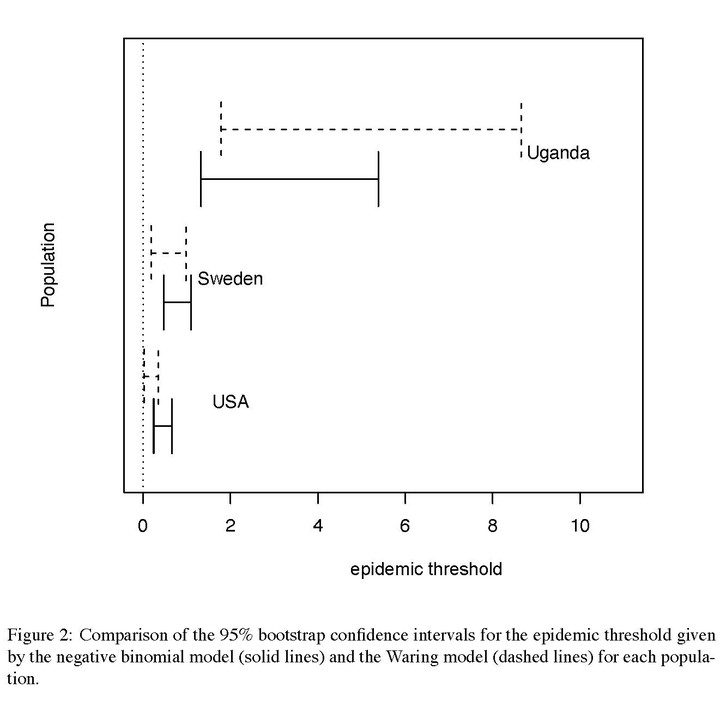
Epidemic thresholds in network models of heterogeneous populations characterized by highly right-skewed contact distributions can be very small. When the population is above the threshold, an epidemic is inevitable and conventional control measures to reduce the transmissibility of a pathogen will fail to eradicate it. We consider a two-sex network model for a sexually transmitted disease which assumes random mixing conditional on the degree distribution. We derive expressions for the basic reproductive number for one and heterogeneous two-population in terms of characteristics of the degree distributions and transmissibility. We calculate interval estimates for the epidemic thresholds for stochastic process models in three human populations based on representative surveys of sexual behavior (Uganda, Sweden, USA). For Uganda and Sweden, the epidemic threshold is greater than zero with high confidence. For the USA, the interval includes zero. We discuss the implications of these findings along with the limitations of epidemic models which assume random mixing.