An Approach to Statistical Spatial-Temporal Modeling of Meteorological Fields” (with discussion)

Abstract

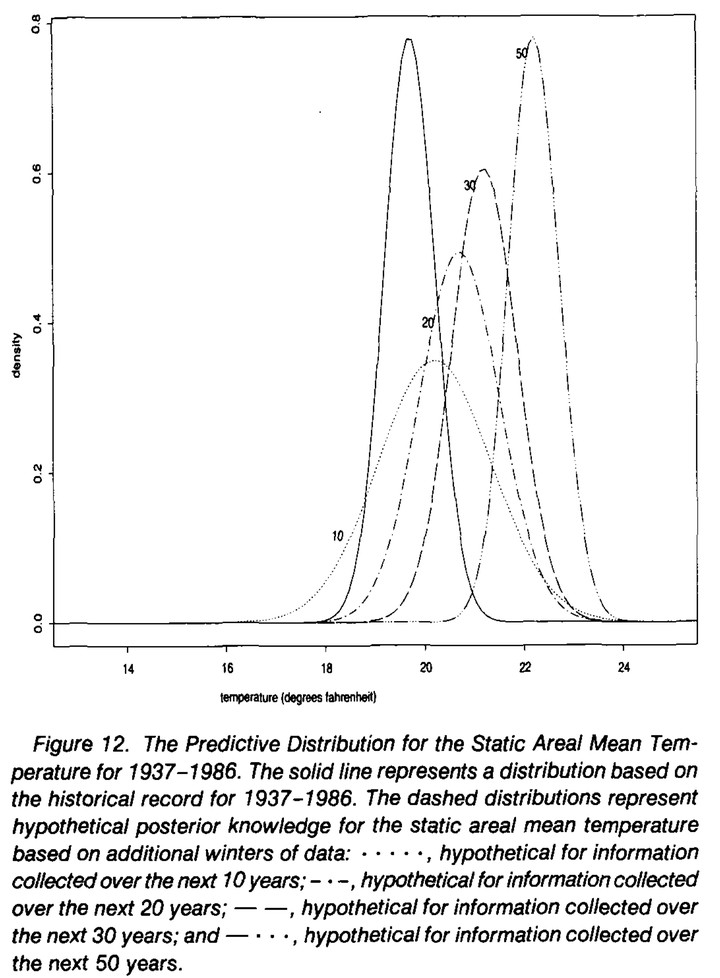
In this article we develop a random field model for the mean temperature over the region in the northern United States covering eastern Montana through the Dakotas and northern Nebraska up to the Canadian border. The readings are temperatures at the stations in the U.S. historical climatological network. The stochastic structure is modeled by a stationary spatial-temporal Gaussian random field. For this region, we find little evidence of temporal dependence while the spatial structure is temporally stable. The approach strives to incorporate the uncertainty in estimating the covariance structure into the predictive distributions and the final inference. As an application of the model, we derive posterior distributions of the areal mean over time. A posterior distribution for the static areal mean is presented as a basis for calibrating temperature shifts by the historical record. For this region and season, the distribution indicates that under the scenario of a gradual increase of $5^\circ F$ over 50 years, it will take 30–40 winters of data before the change will be discernible from the natural variation in temperatures.