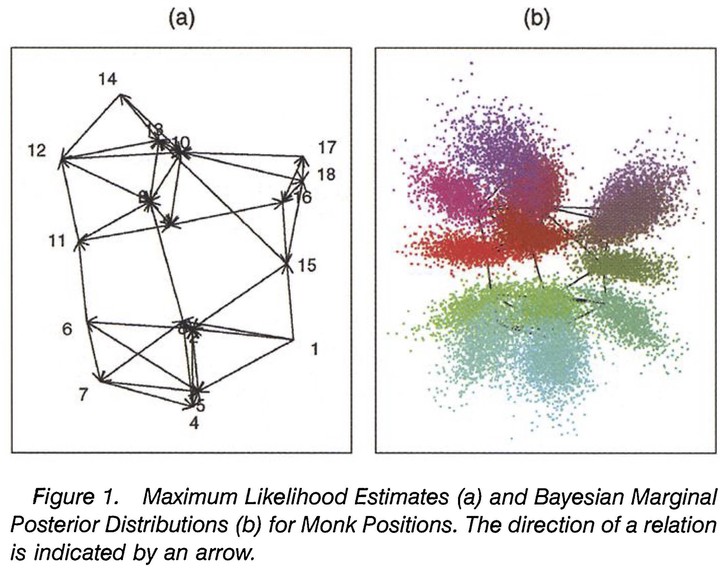
Abstract
Network models are widely used to represent relational information among interacting units. In studies of social networks, recent emphasis has been placed on random graph models where the nodes usually represent individual social actors and the edges represent the presence of a specified relation between actors. We develop a class of models where the probability of a relation between actors depends on the positions of individuals in an unobserved ‘social space.’ We make inference for the social space within maximum likelihood and Bayesian frameworks, and propose Markov chain Monte Carlo procedures for making inference on latent positions and the effects of observed covariates. We present analyses of three standard datasets from the social networks literature, and compare the method to an alternative stochastic blockmodeling approach. In addition to improving on model fit for these datasets, our method provides a visual and interpretable model-based spatial representation of social relationships and improves on existing methods by allowing the statistical uncertainty in the social space to be quantified and graphically represented.