Abstract
Exponential-family Random Graph Models (ERGMs) have long been at the forefront of the analysis of relational data. The exponential-family form allows complex network dependencies to be represented. Models in this class are interpretable, flexible and have a strong theoretical foundation. The availability of powerful user-friendly open-source software allows broad accessibility and use. However, ERGMs sometimes suffer from a serious condition known as near-degeneracy, in which the model exhibits unrealistic probabilistic behavior or a severe lack-of-fit to real network data.
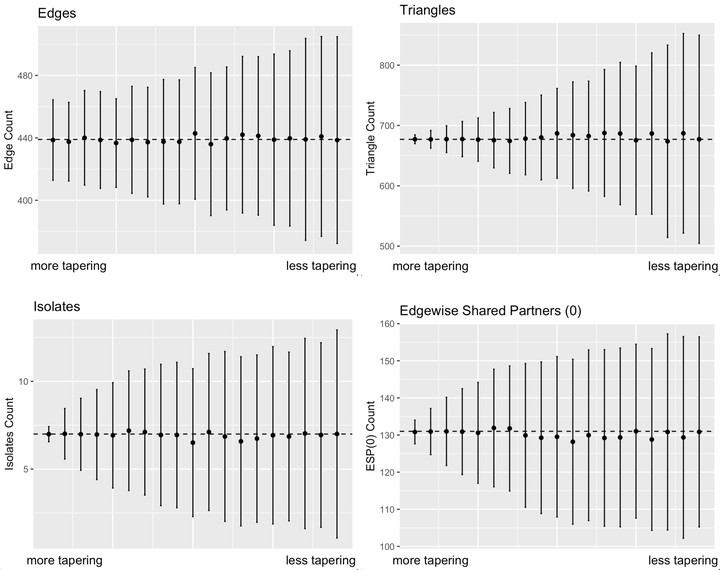
Recently, Fellows and Handcock (2017) proposed a new model class, the Tapered ERGM, which circumvents the issue of near-degeneracy while maintaining the desirable features of ERGMs. However, the question of how to determine the proper amount of tapering needed for any model was heretofore left unanswered. This paper develops a new methodology for how to determine the necessary level of tapering and as such provides a new approach to inference for the Tapered ERGM class. Noting that a Tapered ERGM can always be made non-degenerate, we offer data-driven approaches for determining the amount of tapering necessary. The mean-value parameter estimates are unaffected by tapering, and we show that the natural parameter estimates are numerically weakly varying by the level of tapering. We then apply the Tapered ERGM to two published networks to demonstrate its effectiveness in cases where typical ERGMs fail and present the case for Tapered ERGMs replacing ERGMs entirely.
This is joint work with Bark Blackburn and Ian E. Fellows.